Tuesday, April 19, 2022
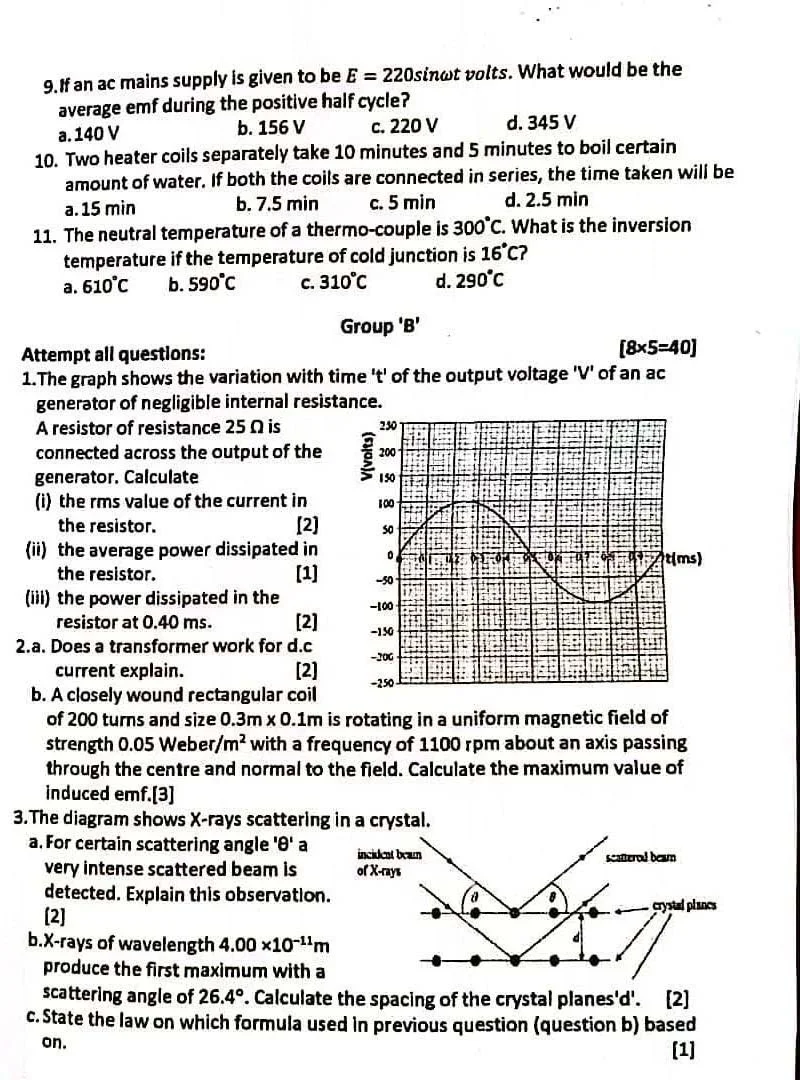
Sunday, April 17, 2022
Diffraction
Subscribe to:
Posts (Atom)
Featured Post
Reflection Through plane surface
Refraction a Refraction through Plane Surface Refraction Refraction of light is the process of bending of light when it passes from one opt...
-
Cell division project Mitosis Cell Division Meiosis Cell Division Differences a VISUALIZATION OF CELL DIVISIO...