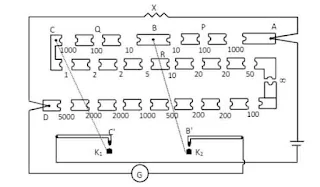
Potentiometer
A potentiometer is an electric device used to measure the emf and internal resistance of a cell, to compare emf of two cells and a potential difference between two points in an electric circuit. It can also be employed to measure the current and resistance in a circuit accurately.
It consists of a uniform wire
let I be the current passing through the potentiometer wire
Then,
let I be the current passing through the potentiometer wire
Then,
where
If 1 is the length of this segment, its resistance is
If 1 is the length of this segment, its resistance is
where
From
From
Since
then
then
The potential difference across any portion of the potential of the potentiometer wire is directly proportional to the length of that portion provided the current is uniform.
Application of Potentiometer
A potentiometer basically measures the potential difference between two points.
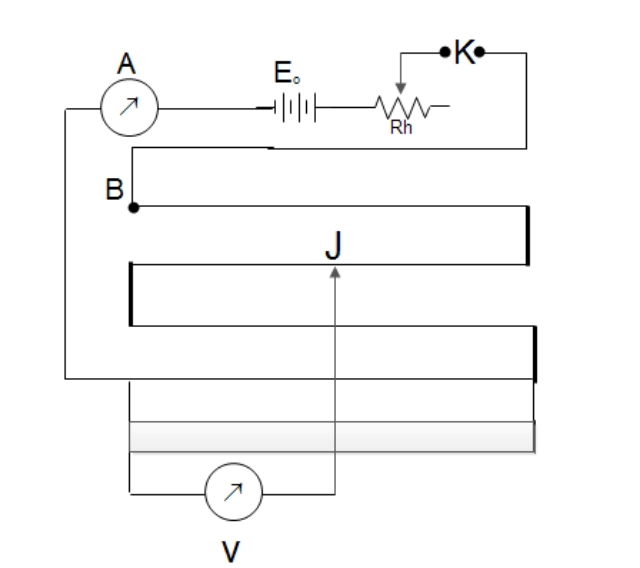
1. Determination of Internal Resistance of a Cell

A cell of emf E whose internal resistance
Initiallly the key is open and the emf
From the principle of potentiometer
Now, a known resistance
If
Dividing equation
and the terminal p.d.,
Substituting these values in equation (iii), we get
Substituting these values in equation (iii), we get
As
2) Comparison of emfs of two Cells and Determination of emf of a Cell
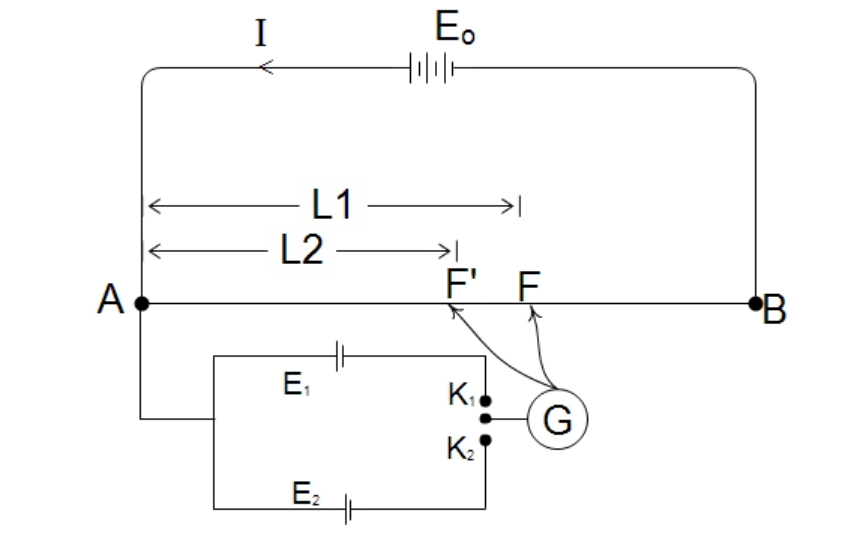
Two cells whose emfs
2) Comparison of emfs of two Cells and Determination of emf of a Cell

Two cells whose emfs
One of the cells say
When the jockey is placed at
When the jockey is placed at
From the principle of potentiometer,
So
So
Similar work is repeated for the next cell,
Dividing
Sincel l1 and
If the emf of one cell, say
If the emf of one cell, say