XII Nepali Model Question

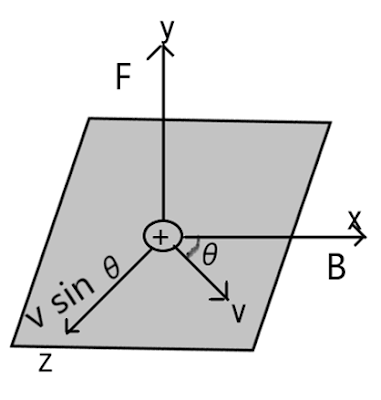
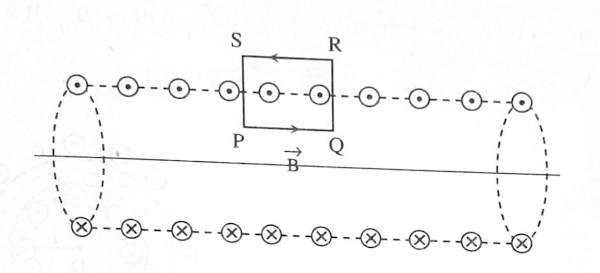
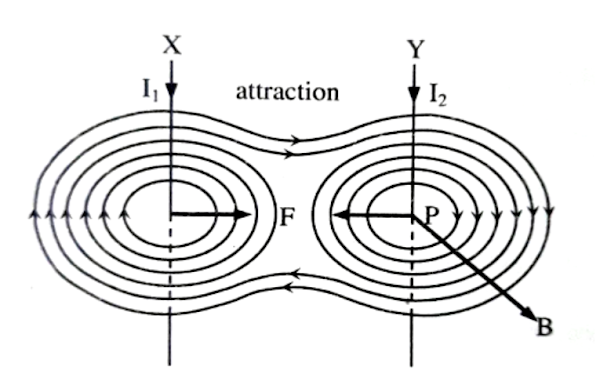
Magnetic Field_Bsc

aMagnetic Field Magnetic Field is the region around a magnetic material or a moving electric charge within which the force of magnetism acts. It is a vector quantity. It is represented by 'B' or 'H' and its unit is tesla (T). Magnetic Lines of ForceMagnetic lines of force (field lines) are imaginary lines around the magnet which shows the path traced by a unit north pole when it is allowed to move freely. A tangent drawn at magnetic lines of force gives the direction of magnetic field.Properties of magnetic lines of force1. Magnetic field lines never cross each other2. The density of the field lines indicates the strength of the field3. Magnetic field lines always make closed loops4. Magnetic field lines always emerge or start from the north pole and terminate at the south pole.

Figure 1:Magnetic Lines of force around a bar magnet

Figure 2:Magnetic lines of force around straight conductor

Figure 3: Magnetic lines of force in a solenoid

Magnetic FluxMagnetic flux ɸ through any surface area in a magnetic field is defined as the number of magnetic lines of force crossing through the surface.

The magnetic flux passing through a surface area A$A$ in a magnetic field B$B$ is given by𝜙=B⋅A=BACos𝜃$$\begin{array}{c}𝜙=\overrightarrow{B}\cdot \overrightarrow{A}\\ =BA\mathrm{C}\mathrm{o}\mathrm{s}𝜃\end{array}$$If 𝜃=0∘$𝜃=0^{\circ }$ then, 𝜙=BA$𝜙=BA$Where: a

𝜙	= magnetic flux (Wb)
B	= magnetic flux density (T)
A	= cross-sectional area (m2)

$$\begin{array}{rl}𝜙& =\text{ magnetic flux }(\mathrm{W}\mathrm{b})\\ B& =\text{ magnetic flux density }(T)\\ A& =\text{ cross-sectional area }\left(m^2\right)\end{array}$$This means the magnetic flux is:Maximum =BA$=BA$ , when cos(𝜃)=1$\cos (𝜃)=1$ therefore 𝜃=0∘$𝜃=0^{\circ }$. The magnetic field lines are perpendicular to the plane of the areaMinimum =0$=0$ when cos(𝜃)=0$\cos (𝜃)=0$ therefore 𝜃=90∘$\mathit{𝜃}={90}^{\circ }$. The magnetic fields lines are parallel to the plane of the area Magnetic Flux Density We Know, Magnetic flux density𝜙=BA$$𝜙=BA$$or B=𝜙

A$B=\frac{𝜙}{A}$Thus, Magnetic field intensity (B) is defined as the magnetic flux (normal) per unit area.Force on a moving Charge in a magnetic Field

When an electric charge moves through a magnetic field, the field exerts a force on the charge. Let us consider a charge +q$+q$ moves with velocity v$v$ in XZ$XZ$ plane with magnetic field B$B$ along x$x$-axis.Experimentally it is found that magnitude of force isi) directly proportional to the magnitude of the chargeF∝q$$F\propto q$$ii) directly proportional to the velocity of the chargeF∝v$$F\propto v$$iii) directly proportional to the strength of the magnetic fieldF∝B$$F\propto B$$iv) directly proportional to the sine of angle between B$B$ and v$v$F∝sin𝜃$$F\propto \sin 𝜃$$Combining allF∝Bqvsin𝜃$$F\propto Bqv\sin 𝜃$$or, F=kBqvsin𝜃$F=kBqv\sin 𝜃$where k$k$ is a proportionality constant whose value is I in SI units.

F=Bqvsin𝜃

In Vector formF=q(v×B) $$\overrightarrow{F}=q(\overrightarrow{v}\times \overrightarrow{B})$$Direction of the ForceThe force is perpendicular to the plane containing v$v$ and B$B$, ie it is along y$y$-axis. It is determined by the Fleming right hand rule.Special Case:F=Bqvsin𝜃$$F=Bqv\sin 𝜃$$i) when 𝜃=0∘$𝜃=0^{\circ }$ or 180∘,sin𝜃=0${180}^{\circ },\sin 𝜃=0$a

	F =Bqv(0)
	=0

$$\begin{array}{rl}& F=Bqv(0)\\ & =0\end{array}$$Hence, F=0$F=0$, if the charge particle is moving parallel or antiparallel to the magnetic field.ii) when 𝜃=90∘$𝜃={90}^{\circ }$F=Bq$F=Bq$, which is max. valueHence, Force is maximum if the charge particle is moving perpendicular to the magnetic field.iii) When v=0, F=0$v=0,F=0$Hence, No force is experienced by an stationary charge.iv) When, q=0$q=0$F=0$$F=0$$Hence, Force is experienced by charged particle only. Force on a current carrying conductor

Let us consider a straight segment of a conductor of length l and cross-sectional area A carrying a steady current I from bottom to top as shown in figure. Let it be placed in a region of uniform magnetic field B$\overrightarrow{B}$ which is parallel to the plane of paper and 𝜃$𝜃$ be its inclination with the direction of field. We have assumed the conventional direction of current and hence the moving charges are positive.Let vd${\mathrm{v}}_{\mathrm{d}}$ be the drift velocity of these charges which also must have an inclination of 𝜃$𝜃$ with the magnetic field. The magnetic Lorentz force experienced by each charge of magnitude q$q$ is given by,a

F	= q(vd×B)
F	=Bqvdsin𝜃 ..............(i)

$$\begin{array}{rl}\overrightarrow{F}& =q(\overrightarrow{v_d}\times \overrightarrow{B})\\ F& =Bq{v}_d\sin 𝜃..............(i)\end{array}$$The direction of this force is into the plane of paper as defined by Fleming's left hand rule.If n$n$ be the number of charge per unit volume of the conductor, the total number of charge in the conductor is,N=nV=nAl................(ii)$$\mathrm{N}=\mathrm{n}\mathrm{V}=\mathrm{n}\mathrm{A}l................(ii)$$So, the total magnetic force experience by all the charges in the conductor is,F=NBqvdsin𝜃……(iii)$$\mathrm{F}=\mathrm{N}\mathrm{B}\mathrm{q}{\mathrm{v}}_{\mathrm{d}}\sin 𝜃\dots \dots (iii)$$From equations (ii) and (iii), we get,5a

F	=(nAl)Bqvdsin𝜃
∴F	=(nqAvd)(Blsin𝜃) .............(iv)

$$\begin{array}{rl}\mathrm{F}& =(\mathrm{n}\mathrm{A}l)\mathrm{B}\mathrm{q}{\mathrm{v}}_{\mathrm{d}}\sin 𝜃\\ \therefore \mathrm{F}& =(\mathrm{n}\mathrm{q}\mathrm{A}{\mathrm{v}}_{\mathrm{d}})(\mathrm{B}l\sin 𝜃).............(iv)\end{array}$$We know, current in the form of drift velocity of the charge particle is given by,I=vdqnA....................(v)$$\mathrm{I}={\mathrm{v}}_{\mathrm{d}}qnA....................(v)$$So, from equations (iv) and (v), we get,a

	F=IBlsin𝜃
	F=I(l×B)

$$\begin{array}{rl}& \mathrm{F}=\mathrm{I}\mathrm{B}l\sin 𝜃\\ & \overrightarrow{\mathrm{F}}=\mathrm{I}(\overrightarrow{l}\times \overrightarrow{\mathrm{B}})\end{array}$$Thus, total force experienced by the conductor placed in uniform magnetic field is perpendicular to both length and field (perpendicularly inward into the plane of paper which contains both l$l$ and B$B$ in this case)Case I. If the conductor is parallel or antiparallel to the field, thena

𝜃	=0∘ or 180∘
∴F	=IBlsin0∘ or IBlsin180∘
F	=0

$$\begin{array}{rl}𝜃& =0^{\circ }\text{ or }{180}^{\circ }\\ \therefore \mathrm{F}& =\mathrm{I}\mathrm{B}l\sin 0^{\circ }\text{ or }\mathrm{I}\mathrm{B}l\sin {180}^{\circ }\\ \mathrm{F}& =0\end{array}$$Thus, a conductor placed parallel to uniform magnetic field experiences no force.Case II$\mathrm{I}{I}_{}$ When the conductor is placed perpendicular to magnetic fielda

𝜃	=90∘
∴F	=IBlsin90∘=BIl

$$\begin{array}{rl}𝜃& ={90}^{\circ }\\ \therefore \mathrm{F}& =\mathrm{I}\mathrm{B}l\sin {90}^{\circ }=\mathrm{B}\mathrm{I}l\end{array}$$This is the maximum force experienced by the conductor.Direction of ForceAs F=I( l×B)$$As\overrightarrow{\mathrm{F}}=\mathrm{I}(\overrightarrow{l}\times \overrightarrow{\mathrm{B}})$$ The direction of force is perpendicular to the plane containing B$B$ and l. It is determined using Fleming's left hand rule. Biot and Savart Law

Consider a conductor XY through which current I is flowing. dl be the length element of conductor. P be any point at a distance r from dl making angle 𝜃${\displaystyle 𝜃}$. Then according to Biot and savart law, the magnetic field at point P due to current I in length element dl is 1) directly propoetional to the current dB∝ I${\displaystyle dB\propto I}$2) directly proportional to length of the length element dB∝ dl${\displaystyle dB\propto dl}$3) directly proportional to sine of the angle between the conductor and the line joining r$r$ dB∝ sin𝜃${\displaystyle dB\propto sin𝜃}$4) inversely proportional to square of the distance between the element and the point P$P$ dB∝ 1

r2 ${\displaystyle dB\propto \frac{1}{r^2}}$Combining above equations, we geta

dB	∝Idlsin𝜃 r2
dB	=kIdlsin𝜃 r2

$$\begin{array}{rl}\mathrm{d}\mathrm{B}& \propto \frac{I\mathrm{d}l\sin 𝜃}{r^2}\\ \mathrm{d}\mathrm{B}& =\frac{kIdl\sin 𝜃}{r^2}\end{array}$$where k$k$ is proportionality constant. In SI-units, k=𝜇0

4𝜋$k=\frac{{𝜇}_0}{4{𝜋}^{}}$ The constant 𝜇0${𝜇}_0$ is the permeability of free space and has value 4𝜋×10-7$4𝜋\times {10}^{-7}$ henry per meter, So, we can writedB=𝜇0

4𝜋Idsin𝜃

r2$$dB=\frac{{𝜇}_0}{4𝜋}\frac{Id\sin 𝜃}{r^2}$$Biot and Savart Law in Vector FormIf we consider length of the element as dl$d\overrightarrow{l}$, distance of P$\mathrm{P}$ as displacement vector r$\overrightarrow{r}$ and unit vector along CP us r ${\widehat{r}}_{}$thena

dB=𝜇0 4𝜋Idl×r r2

dB=𝜇0 4𝜋I(dl×r) r3

$$\begin{array}{c}d\overrightarrow{B}=\frac{{𝜇}_0}{4𝜋}\frac{Id\overrightarrow{l}\times \widehat{r}}{r^2}\\ d\overrightarrow{B}=\frac{{𝜇}_0}{4𝜋}\frac{I(d\overrightarrow{l}\times \overrightarrow{r})}{r^3}\end{array}$$where unit vector, r=r

|r|=r

r$\widehat{r}=\frac{\overrightarrow{r}}{|\overrightarrow{r}|}=\frac{\overrightarrow{r}}{r}$. The element vector dl$d\overrightarrow{l}$ has direction in the direction of the current.Application of Biot Savart Law1. Magnetic Field at hte centre fo the current carrying circular coil

Consider a circular coil of radius r. Let N be the number of turns of the coil and I${\displaystyle I}$ be the current flowing throught the coil, then according to Biot -Savart law magnetic field at the dentre of coil due to small elemnt dl${\displaystyle dl}$ is given by, dB = 𝜇o

4𝜋 Idlsin𝜃

r2${\displaystyle dB=\frac{{𝜇}_o}{4𝜋}\frac{Idlsin𝜃}{r^2}}$since, the radius r is perpendicular to length element dl${\displaystyle dl}$𝜃=900${\displaystyle 𝜃={90}^0}$so dB = 𝜇o

4𝜋 Idl

r2${\displaystyle dB=\frac{{𝜇}_o}{4𝜋}\frac{Idl}{r^2}}$ ..........(i)Now the total magnetic field 'B', due to a whole circular coil is obtained by integrating eqn. (i) from 0 to 2𝜋r${\displaystyle 2𝜋r}$B=∫dB${\displaystyle B=\int dB}$B = 2𝜋r∫0𝜇o

4𝜋 Idl

r2${\displaystyle B=\underset{0}{\overset{2𝜋r}{\int }}\frac{{𝜇}_o}{4𝜋}\frac{Idl}{r^2}}$ =𝜇oI

4𝜋r2 2𝜋r∫0 dl${\displaystyle =\frac{{𝜇}_{o}I}{4𝜋r^2}\underset{0}{\overset{2𝜋r}{\int }}dl}$=𝜇oI

4𝜋r2 [dl]2𝜋r0${\displaystyle =\frac{{𝜇}_{o}I}{4𝜋r^2}[dl{]}_0^{2𝜋r}}$=𝜇oI

4𝜋r2 [ 2𝜋r - 0]${\displaystyle =\frac{{𝜇}_{o}I}{4𝜋r^2}[2𝜋r-0]}$=𝜇oI2𝜋r

4𝜋r2 ${\displaystyle =\frac{{𝜇}_{o}I2𝜋r}{4𝜋r^2}}$=𝜇oI

2r${\displaystyle =\frac{{𝜇}_{o}I}{2r}}$The magnetic field due to total, N number of turns of coil is,

B = 𝜇0NI

2r

Direction of BThe magnetic field produce is perpendicular to the plane of coil. At the centre of coil it is pointed inward to the plane of paper. 2. Magnetic Field on the axis of Current carrying circular coil

Let there be a circular coil of radius 'a' and carrying current 'I'${\displaystyle \text{'}I\text{'}}$. Let P be any point on the axis of a coil at a distance 'x' from the center and which we have to find the field. To calculate the field consider a current element dl${\displaystyle dl}$ at the top of the coil pointing perpendicularly outward from plane of paper. Then according to Biot Savart Law, the magnetic field due to length element dl ${\displaystyle dl}$ is given bydB = 𝜇o

4𝜋 Idlsin𝛼

r2${\displaystyle dB=\frac{{𝜇}_o}{4𝜋}\frac{Idlsin𝛼}{r^2}}$.........................(i)Here, angle 𝛼${\displaystyle 𝛼}$ between dl ${\displaystyle dl}$ and 'r' can be taken as 𝜋

2.${\displaystyle \frac{𝜋}{2}.}$ So the equation (i) becomes,dB = 𝜇o

4𝜋 Idl

r2${\displaystyle dB=\frac{{𝜇}_o}{4𝜋}\frac{Idl}{r^2}}$This, magnetic field dB, is perpendicular to dl${\displaystyle dl}$ and r both as shown in figure. dB can be resolved in to components, dBcos𝜃${\displaystyle dBcos𝜃}$ and dBsin𝜃${\displaystyle dBsin𝜃}$. The vertical components ${\displaystyle }$dBcos𝜃${\displaystyle dBcos𝜃}$ cancle each other being equal and opposite. So only the horizontal component dBsin𝜃${\displaystyle dBsin𝜃}$ contibute to the total magnetic field.so, total magnetic field due to whole coil is given by integratind dB from 0 to 2𝜋a${\displaystyle 2𝜋a}$ ${\displaystyle }$B = ∫dB${\displaystyle B=\int dB}$ =2𝜋a∫0𝜇o

4𝜋 Idl

r2sin𝜃${\displaystyle \underset{0}{\overset{2𝜋a}{\int }}\frac{{𝜇}_o}{4𝜋}\frac{Idl}{r^2}sin𝜃}$ =𝜇o

4𝜋 I

r2sin𝜃2𝜋a∫0dl${\displaystyle \frac{{𝜇}_o}{4𝜋}\frac{I}{r^2}sin𝜃\underset{0}{\overset{2𝜋a}{\int }}dl}$ = 𝜇o

4𝜋 I

r2sin𝜃 [l]2𝜋a 0${\displaystyle \frac{{𝜇}_o}{4𝜋}\frac{I}{r^2}sin𝜃[l{]}_0^{2𝜋a}}$ = 𝜇o

4𝜋 I

r2sin𝜃 [2𝜋a - 0] ${\displaystyle \frac{{𝜇}_o}{4𝜋}\frac{I}{r^2}sin𝜃[2𝜋a-0]}$ = 𝜇oIa

2r2sin𝜃 ${\displaystyle \frac{{𝜇}_{o}Ia}{2r^2}sin𝜃}$From the figure, sin𝜃 = a

r ${\displaystyle sin𝜃=\frac{a}{r}}$so, B = 𝜇oIa

2r2.a

r ${\displaystyle \frac{{𝜇}_{o}Ia}{2r^2}.\frac{a}{r}}$or, B = 𝜇oIa2

2r3 ${\displaystyle \frac{{𝜇}_{o}I{a}^2}{2r^3}}$As, r=(a2+x2)${\displaystyle r=\sqrt{(a^2}+x^2)}$so, B = 𝜇oIa2

2(a2+x2)3/2 ${\displaystyle \frac{{𝜇}_{o}I{a}^2}{2(a^2+x^2{)}^{3/2}}}$If the coil has N number of turns

B = 𝜇oNIa2

2(a2+x2)3/2

Special Case,i) when point P is at the centre of the coil x = 0 so B = 𝜇oNIa 2

2(a2)3/2 = 𝜇oNI

2a Which is the expression for the magnetic field at the centre of a circular coil.ii) When point P is far away from the centre of the coil, in such case, x≫ a so that B = 𝜇oNIa2

2(x2)3/2 B = 𝜇oNIa2

2x3Direction of BAs the current is in anticlockwise direction, the magnetic field at the axis is the coil is pointing right towards positive x- axis. ( By applying right hand thumb rule). 3. Magnetic Field due to straight current carrying conductor

Let us take a straight conductor, XY carrying current (I) in upward direction. We have to calculate magnetic field at point (P) at a distance (a) from the straight conductor i.e. OP = a. Let us take small element of length (dl${\displaystyle dl}$) at point (C) i.e. OC = l${\displaystyle OC=l}$ Let us join C and P i.e. CP = r In figure, ∠OPC = 𝜃${\displaystyle \angle OPC=𝜃}$and ∠OCP= 𝜙${\displaystyle \angle OCP=𝜙}$ According to Biot and Savart law, the magnetic field at point P due to small element the (dl${\displaystyle dl}$) at point (C) is dB=𝜇0

4𝜋Idl sin 𝜙

r2 ................(i)$$\mathrm{d}\mathrm{B}=\frac{{𝜇}_0}{4𝜋}\frac{I\mathrm{d}lsin𝜙}{{\mathrm{r}}^2}................(i)$$Then in Δ POC${\displaystyle \Delta POC}$sin𝜙=a

r=cos𝜃$\sin 𝜙=\frac{a}{\mathrm{r}}=\cos 𝜃$or r=a

cos𝜃$r=\frac{a}{\cos 𝜃}$Also, tan𝜃=l

a$\tan 𝜃=\frac{l}{a}$or l=atan𝜃$l=a\tan 𝜃$Differentiating both sides with respect to 𝜃$𝜃$, we get or dl=asec2𝜃d𝜃$$\text{ or }dl=a{\sec }^2𝜃d𝜃$$Putting these values in eqn. (i) dB=𝜇0

4𝜋I(asec2𝜃d𝜃)

(a2

cos2𝜃)cos𝜃$$\mathrm{d}\mathrm{B}=\frac{{𝜇}_0}{4𝜋}\mathrm{I}\frac{\left(\mathrm{a}{\sec }^2𝜃\mathrm{d}𝜃\right)}{\left(\frac{{\mathrm{a}}^2}{{\cos }^2𝜃}\right)}\cos 𝜃$$ a

=𝜇0 4𝜋Iasec2𝜃d𝜃 a2cos2𝜃cos𝜃

dB=𝜇0 4𝜋Icos𝜃d𝜃 a ........................(ii)

$$\begin{array}{l}=\frac{{𝜇}_0}{4𝜋}\frac{\mathrm{I}\mathrm{a}{\sec }^2𝜃\mathrm{d}𝜃}{{\mathrm{a}}^2}{\cos }^2𝜃\cos 𝜃\\ \mathrm{d}\mathrm{B}=\frac{{𝜇}_0}{4𝜋}\frac{\mathrm{I}\mathrm{c}\mathrm{o}\mathrm{s}𝜃\mathrm{d}𝜃}{\mathrm{a}}........................(ii)\end{array}$$Magnetic field due to whole conductor AB can be calculated by integrating Eq. (ii)$(ii)$ from -𝜃1$-{𝜃}_1$ to 𝜃2${𝜃}_2$. (By convention 𝜃1${𝜃}_1$, being anticlock-wise is taken as negative). a

B=𝜃2∫-𝜃1dB

=𝜇0I 4𝜋a𝜃2∫-𝜃1cos𝜃d𝜃

= mal4𝜋[sin𝜃]𝜃2-𝜃1 4𝜋

=𝜇0I 4𝜋⋅a[sin𝜃2-sin(-𝜃1)]

B=𝜇0I 4𝜋a(sin𝜃2+sin𝜃1)

B=𝜇0I 4𝜋a(sin𝜃1+sin𝜃2) ............(iii)

$$\begin{array}{l}B=\underset{-𝜃1}{\overset{𝜃2}{\int }}dB\\ =\frac{{𝜇}_{0}I}{4𝜋a}\underset{-𝜃1}{\overset{𝜃2}{\int }}\cos 𝜃d𝜃\\ =\frac{{\mathrm{m}\mathrm{a}\mathrm{l}}_{4𝜋}[\sin 𝜃{]}_{-{𝜃}_1}^{{𝜃}_2}}{4𝜋}\\ =\frac{{𝜇}_{0}I}{4𝜋\cdot a}[\sin {𝜃}_2-\sin (-{𝜃}_1)]\\ B=\frac{{𝜇}_{0}I}{4𝜋a}(\sin {𝜃}_2+\sin {𝜃}_1)\\ \boxed{B=\frac{{𝜇}_{0}I}{4𝜋a}(\sin {𝜃}_1+\sin {𝜃}_2)}............(iii)\end{array}$$This gives the value of B$B$ at point P$P$ due to a conductor of finite length.If the conductor of infinite length is taken,𝜃1=𝜃2=𝜋/2${𝜃}_1={𝜃}_2=𝜋/2$.a

B= 𝜇0I 4𝜋a(sin𝜋/2+sin𝜋/2)=𝜇0I 4𝜋a(1+1)

B=𝜇0I 2𝜋a

$$\begin{array}{l}B=\frac{{𝜇}_{0}I}{4𝜋a}(\sin 𝜋/2+\sin 𝜋/2)=\frac{{𝜇}_{0}I}{4𝜋a}(1+1)\\ B=\frac{{𝜇}_{0}I}{2𝜋a}\end{array}$$ Direction of BThe direction of magnetic field B is obtained by using right hand rule which is directed inward to the plane of paper.4. Magnetic Field due to a solenoid

Let us consider a solenoid of radius 'a' having 'n' number of turns per unit length. Current 'I'${\displaystyle \text{'}I\text{'}}$ flows through the solenoid as shown in the diagram. Let 'P' be any any point on its axis. XY be length element of length dl${\displaystyle dl}$ which makes angle d𝜃${\displaystyle d𝜃}$ at point P. From the figure, XP = r, XD =a , and ∠XPD = 𝜃${\displaystyle \angle XPD=𝜃}$. Since magnetic field produced by a single coil is B=𝜇0Ia sin 𝜃

2r2$B=\frac{{𝜇}_{0}Iasin𝜃}{2r^2}$ so a small magnetic field produce by$by$ the element dl$dl$ having ndl${\displaystyle ndl}$ turns at point P$P$ is given bydB=𝜇0Iasin𝜃

2r2ndl ..............(i)$$\mathrm{d}\mathrm{B}=\frac{{𝜇}_0\mathrm{I}\mathrm{a}\sin 𝜃}{2{\mathrm{r}}^2}\mathrm{n}\mathrm{d}l..............(i)$$Here, for small length dl${\displaystyle dl}$, XP≈YP =r${\displaystyle XP\approx YP=r}$In 𝛥YCP$𝛥\mathrm{Y}\mathrm{C}\mathrm{P}$, sin d𝜃= YC

YP=YC

r${\displaystyle sind𝜃=\frac{YC}{YP}=\frac{YC}{r}}$we have for small angle d𝜃,$\mathrm{d}𝜃,$, sind𝜃=d𝜃${\displaystyle sind𝜃=d𝜃}$.so, d𝜃= YC

r${\displaystyle d𝜃=\frac{YC}{r}}$or, YC= rd𝜃${\displaystyle YC=rd𝜃}$In 𝛥XYC, sin𝜃=YC

XY=YC

dl$𝛥XYC,\sin 𝜃=\frac{YC}{XY}=\frac{YC}{dl}$or YC=dlsin𝜃$\mathrm{Y}\mathrm{C}=\mathrm{d}l\sin 𝜃$Then, we have,a

rd𝜃	=dlsin𝜃
or dl	=rd𝜃 sin𝜃.

$$\begin{array}{rl}\mathrm{r}\mathrm{d}𝜃& =\mathrm{d}l\sin 𝜃\\ \text{ or }\mathrm{d}l& =\frac{\mathrm{r}\mathrm{d}𝜃}{\sin 𝜃}.\end{array}$$Using value of dl$\mathrm{d}l$ in Eq. (i), we geta

dB	=𝜇0Iasin𝜃 2r2nrd𝜃 sin𝜃
or dB	=𝜇0Ian 2rd𝜃

$\begin{array}{rl}\mathrm{d}\mathrm{B}& =\frac{{𝜇}_0\mathrm{I}\mathrm{a}\sin 𝜃}{2{\mathrm{r}}^2}\mathrm{n}\frac{\mathrm{r}\mathrm{d}𝜃}{\sin 𝜃}\\ \text{ or }\mathrm{d}\mathrm{B}& =\frac{{𝜇}_0\mathrm{I}\mathrm{a}\mathrm{n}}{2\mathrm{r}}\mathrm{d}𝜃\end{array}$Again from △XDP$△\mathrm{X}\mathrm{D}\mathrm{P}$,a

sin𝜃=a r

r=a sin𝜃.

$$\begin{array}{l}\sin 𝜃=\frac{a}{r}\\ r=\frac{a}{\sin 𝜃}.\end{array}$$Putting value of r$\mathrm{r}$ in (i), we geta

dB	=𝜇0I a nd𝜃 2sin𝜃 a
or dB	=𝜇0nIsin𝜃 2d𝜃.............(ii)

$\begin{array}{rl}\mathrm{d}\mathrm{B}& =\frac{{𝜇}_0\mathrm{I}\text{ a }\mathrm{n}\mathrm{d}𝜃}{2}\frac{\sin 𝜃}{\mathrm{a}}\\ \text{ or }\mathrm{d}\mathrm{B}& =\frac{{𝜇}_0\mathrm{n}\mathrm{I}\sin 𝜃}{2}\mathrm{d}𝜃.............(ii)\end{array}$If the radius voctor r$r$ makes angles 𝜙1${𝜙}_1$ and 𝜙2${𝜙}_2$ at P$P$ from two ends of coil, the total magnetic field at point P$P$ can be obtained by integrating Eq$Eq$. (ii) from 𝜙1${𝜙}_1$ to 𝜙2${𝜙}_2$. Soa

B	=𝜙2 ∫𝜙1𝜇0nIsin𝜃 2d𝜃
	=𝜇0nI 2𝜙2∫𝜙1sin𝜃d𝜃
	=𝜇0nI 2[-cos𝜃]𝜙2𝜙1
B	=𝜇0nI 2(cos𝜙1-cos𝜙2)..........(iii)

$$\begin{array}{rl}B& =\underset{𝜙1}{\overset{𝜙2}{\int }}\frac{{𝜇}_0\mathrm{n}\mathrm{I}\sin 𝜃}{2}\mathrm{d}𝜃\\ & =\frac{{𝜇}_0\mathrm{n}\mathrm{I}}{2}\underset{𝜙1}{\overset{𝜙2}{\int }}\sin 𝜃\mathrm{d}𝜃\\ & =\frac{{𝜇}_0\mathrm{n}\mathrm{I}}{2}[-\cos 𝜃{]}_{{𝜙}_1}^{{𝜙}_2}\\ B& =\frac{{𝜇}_0\mathrm{n}\mathrm{I}}{2}(\cos {𝜙}_1-\cos {𝜙}_2)..........(iii)\end{array}$$If the solenoid is very long then 𝜙1=0∘${𝜙}_1=0^{\circ }$ and 𝜙2=𝜋${𝜙}_2=𝜋$. So Eq. (iii) becomes,a

B=𝜇0nI 2(cos0∘-cos𝜋)= 𝜇0nI 2(1+1)

∴B=𝜇0nI

$$\begin{array}{l}B=\frac{{𝜇}_{0}nI}{2}(\cos 0^{\circ }-\cos 𝜋)=\frac{{𝜇}_{0}nI}{2}(1+1)\\ \therefore B={𝜇}_{0}nI\end{array}$$Direction of B: Direction of B can be determined by right hand first rule. Hence direction of the field is along the axis DP of the solenoid. Ampere's LawAmpere's law is an alternative to Biot and Savart law. However, it is useful for calculating magnetic field only in situations with symmetric condition. The law states that the line integral of the magnetic field around any closed path in free space is equal to 𝜇0${𝜇}_0$ times the total current enclosed by the path,∮B⋅dl=𝜇0I$$\oint \overrightarrow{\mathrm{B}}\cdot \mathrm{d}\overrightarrow{l}={𝜇}_0\mathrm{I}$$where 𝜇0${𝜇}_0$ is permeability of free space, B$\overrightarrow{\mathrm{B}}$ is magnetic field, dl$\mathrm{d}l$ is the small element and I$\mathrm{I}$ is current. The closed path is called Amperian loop.Proof: Consider a straight conductor carrying current I${\displaystyle I}$ as shown in figure. The conductor produces magnetic field in which the magnetic lines of force are concentric circles with centre at the conductor.

Magnitude of magnetic field at P$\mathrm{P}$ at a distance r$\mathrm{r}$ from the conductor is given byB=𝜇0I

2𝜋r$$\mathrm{B}=\frac{{𝜇}_0\mathrm{I}}{2𝜋\mathrm{r}}$$Let the closed loop is a circle of radius r. XY be a small element of length dl${\displaystyle dl}$. Since B is tangent at every point on the loop, so dl${\displaystyle dl}$ and B are in same direction. Therefore, the line integral of B$\overrightarrow{B}$ over this closed loop is given by ∮B⋅dl=∮Bdlcos0∘=∮Bdl$$\oint \overrightarrow{\mathrm{B}}\cdot \mathrm{d}\overrightarrow{l}=\oint \mathrm{B}\mathrm{d}l\cos 0^{\circ }=\oint \mathrm{B}\mathrm{d}l$$Substituting value of B$B$ in above equation,a

	∮B⋅dl=∮ 𝜇0I 2𝜋rdl=𝜇0I 2𝜋r∮dl=𝜇0I 2𝜋r2𝜋r
∴	∮B⋅dl=𝜇0I

$$\begin{array}{rl}& \oint \overrightarrow{\mathrm{B}}\cdot \mathrm{d}\overrightarrow{l}=\oint \frac{{𝜇}_0\mathrm{I}}{2𝜋\mathrm{r}}\mathrm{d}l=\frac{{𝜇}_0\mathrm{I}}{2𝜋\mathrm{r}}\oint \mathrm{d}l=\frac{{𝜇}_0\mathrm{I}}{2𝜋\mathrm{r}}2𝜋\mathrm{r}\\ \therefore & \oint \overrightarrow{\mathrm{B}}\cdot \mathrm{d}\overrightarrow{l}={𝜇}_0\mathrm{I}\end{array}$$This proves Ampere's law. In second figure, current I2${\mathrm{I}}_2$ is passing in opposite to I1${\mathrm{I}}_1$, then the currents enclosed by the loop is (I1-I2)$({\mathrm{I}}_1-{\mathrm{I}}_2)$. Ampere's law is then given by,∮B⋅dl=𝜇0(I1-I2)$$\oint \overrightarrow{\mathrm{B}}\cdot \mathrm{d}\overrightarrow{l}={𝜇}_0({\mathrm{I}}_1-{\mathrm{I}}_2)$$Note: In order to use this law, it is necessary to choose a closed path for which it is possible to determine the line integral of B$\overrightarrow{B}$. For this reason, this law has limited use. This law is not a universal law and cannot be used to find out magnetic field at the centre of the current carrying loop. Applications of Ampere's Law 1. Magnetic field due to a straight current carrying conductor:

Consider a long straight conductor carrying current I${\displaystyle I}$ as shown in figure. It is desired to find out the magnetic field at a point P$P$ at a perpendicular distance r$r$ from the conductor. The magnetic lines of force are concentric circles centred at the conductor. If we choose a circle of radius r$r$ as the closed path, the magnitude of B$\overrightarrow{\mathrm{B}}$ at every point on the path is same. The field B$\overrightarrow{\mathrm{B}}$ is tangent to dl$\mathrm{d}\overrightarrow{l}$ and at every point on the circle. Thus applying Ampere's law to this closed path, we get∮B⋅dl=𝜇0I$\oint \overrightarrow{\mathrm{B}}\cdot \mathrm{d}\overrightarrow{l}={𝜇}_0\mathrm{I}$or ∮B⋅dlcos0∘=𝜇0I$\oint \mathrm{B}\cdot \mathrm{d}l\cos 0^{\circ }={𝜇}_0\mathrm{I}$or B∮dl=𝜇0I$\mathrm{B}\oint \mathrm{d}l={𝜇}_0\mathrm{I}$or B2𝜋r=𝜇0I$\mathrm{B}2𝜋\mathrm{r}={𝜇}_0\mathrm{I}$ B=𝜇0I

2𝜋r$\mathrm{B}=\frac{{𝜇}_0\mathrm{I}}{2𝜋\mathrm{r}}$This is the same expression as obtained by using Biot and Savart law.2. Magnetic Field due to current carrying solenoid

Consider a very long solenoid having 'n' number of turns per unit length. Let current I${\displaystyle I}$ be current flowing through the solenoid, so that a magenetic field 'B' is produced. Inside the solenoid, the magnetic field (B) is uniform, strong and directed along the axis of the solenoid. The magnetic field outside the solenoid is very weak and can be neglected.In order to use Ampere's law to determine the magnetic field inside the solenoid, let us draw a dosed path PQRS$\mathrm{P}\mathrm{Q}\mathrm{R}\mathrm{S}$ as shown in the figure, where PQ=l$\mathrm{P}\mathrm{Q}=l$. The line integral of B$\overrightarrow{\mathrm{B}}$ over the closed path PQRS$PQRS$ is given by, ∮B⋅dl=Q∫PB .dl+R∫QB.dl+S∫RB.dl+P∫SB.dl ..............(i)$$\oint \overrightarrow{\mathrm{B}}\cdot \mathrm{d}\overrightarrow{l}=\underset{P}{\overset{Q}{\int }}\overrightarrow{\mathrm{B}}.\mathrm{d}\overrightarrow{l}+\underset{Q}{\overset{R}{\int }}\overrightarrow{\mathrm{B}}.\mathrm{d}\overrightarrow{l}+\underset{R}{\overset{S}{\int }}\overrightarrow{\mathrm{B}}.\mathrm{d}\overrightarrow{l}+\underset{S}{\overset{P}{\int }}\overrightarrow{\mathrm{B}}.\mathrm{d}\overrightarrow{l}..............(i)$$Now, Q∫PB⋅dl=Q∫PBdlcos0∘ =Bl$\underset{P}{\overset{Q}{\int }}\overrightarrow{\mathrm{B}}\cdot \mathrm{d}\overrightarrow{l}=\underset{P}{\overset{Q}{\int }}\mathrm{B}\mathrm{d}l\cos 0^{\circ }=\mathrm{B}l$And, R∫QB⋅dl=P∫SB.dl=0$\underset{Q}{\overset{R}{\int }}\overrightarrow{\mathrm{B}}\cdot \mathrm{d}\overrightarrow{l}=\underset{S}{\overset{P}{\int }}\overrightarrow{\mathrm{B}}.\mathrm{d}\overrightarrow{l}=0$ ( since QR is perpendicular to B)Also S∫RB⋅d l=0$\underset{R}{\overset{S}{\int }}\overrightarrow{\mathrm{B}}\cdot \mathrm{d}\overrightarrow{l}=0$ ( Magnetic field outside the solenoid is considered negligible.)∮B⋅dl=Bl$\oint \overrightarrow{\mathrm{B}}\cdot \mathrm{d}\overrightarrow{l}=\mathrm{B}l$ ..............(ii)According to Ampere's law, we have∮B⋅dl=𝜇0×$\oint \overrightarrow{\mathrm{B}}\cdot d\overrightarrow{l}={𝜇}_0\times$ net current enclosed by the loop PQRSP=𝜇0×$={𝜇}_0\times$ number of turns in PQRSP ×I $\times I$∮B⋅dl=𝜇0nlI$\oint \overrightarrow{\mathrm{B}}\cdot \mathrm{d}\overrightarrow{l}={𝜇}_0\mathrm{n}l\mathrm{I}$ .......................(iii)From Eqs.(ii)$\mathrm{E}\mathrm{q}\mathrm{s}.(ii)$ and (iii)$(iii)$, we getBl=𝜇0nlI$\mathrm{B}l={𝜇}_0\mathrm{n}l\mathrm{I}$B=𝜇0nI $\mathrm{B}={𝜇}_0\mathrm{n}\mathrm{I}$3. Magnetic field due to a current carrying Toroid

A toroid is just a circular solenoid (doughnuts shaped) whose both ends are joined together. Generally, a toroid is a circular hollow ring on which several copper wires are wrapped closely with no gaps between the turns.Let us consider a toroid of radius 'r' with current 'I' ${\displaystyle \text{'}I\text{'}}$. . Let us consider a closed path inside the toroid (Ampere's loop). The magnetic field B is same everywhere on the closed loop. The magnetic field is tangent to the loop and thus angle between B${\displaystyle \overrightarrow{B}}$ and dl${\displaystyle \overrightarrow{dl}}$ is zero. Thus line integral over the closed loop is ∮B.dl= ∮B dl cos 00 = B ⨯2𝜋r${\displaystyle \oint \overrightarrow{B}.\overrightarrow{dl}=\oint Bdlcos{0}^0=B⨯2𝜋r}$ According to Ampere's law, ∮B.dl = 𝜇0 ⨯ net current enclosed by the closed loop${\displaystyle \oint \overrightarrow{B}.\overrightarrow{dl}={𝜇}_0⨯netcurrentenclosedbytheclosedloop}$If toroid has total N number of turns, then total current =N I${\displaystyle =NI}$so, ∮B .dl = 𝜇0 ⨯ N I${\displaystyle \oint \overrightarrow{B}.\overrightarrow{dl}={𝜇}_0⨯NI}$or, B⨯2𝜋r = 𝜇0 ⨯ N I${\displaystyle B⨯2𝜋r={𝜇}_0⨯NI}$or, B=𝜇0 I N

2𝜋r${\displaystyle B=\frac{{𝜇}_{0}IN}{2𝜋r}}$or,

B = 𝜇0 n I

${\displaystyle \boxed{B={𝜇}_{0}nI}}$where, n=N

2𝜋r${\displaystyle n=\frac{N}{2𝜋r}}$is the no of turns per unit length. Force between two parallel current carrying conductorsi) When current pass in same direction

Let us consider two very long parallel conductors X and Y carrying current I1${\displaystyle I_1}$ and I2${\displaystyle I_2}$ respectivelly in the same direction and are seperated by a distance 'r'.The magnetic field at point P (on Y) due to current I1 ${\displaystyle I_1}$flowing in X isBx = 𝜇0I1

2𝜋r.............(i)${\displaystyle B_x=\frac{{𝜇}_0{I}_1}{2𝜋r}.............(i)}$The direction of magnetic field is perpendicular to the plane of paper and is directed outward.Here, Current I2 ${\displaystyle I_2}$is flowing in conductor Y, placed in the magnetic field due to current in conductor X.The force experienced by Y due to current in length element dl${\displaystyle dl}$ of Y isFY=BX I2dl${\displaystyle F_Y=B_X{I}_{2}dl}$or, FY=𝜇0I1

2𝜋r I2dl${\displaystyle F_Y=\frac{{𝜇}_0{I}_1}{2𝜋r}{I}_{2}dl}$The force per unit lenght on Y is FY

dl=𝜇0

2𝜋rI1 I2${\displaystyle \frac{F_Y}{dl}=\frac{{𝜇}_0}{2𝜋r}{I}_1{I}_2}$or,

F=𝜇0

2𝜋r I1I2

${\displaystyle \boxed{F=\frac{{𝜇}_0}{2𝜋r}{I}_1{I}_2}}$This is a force on Y due to conductor x and is directed towards X.Similarly, The force on X due to current flowing in conductor Y is

F=𝜇0

2𝜋r I1I2

${\displaystyle \boxed{F=\frac{{𝜇}_0}{2𝜋r}{I}_1{I}_2}}$This force is ditected towards conductor Y.Thus, the force in the conductors is attractive, when current flows in same direction.ii). When current pass in opposite direction

If the current in the conductor flow in opposite direction then it is found that,FX=-FY${\displaystyle F_X=-F_Y}$It means that the force produced in the conductor have same magnitude but in opposite direction. Thus there is repulsive force between two conductors with current in opposite direction. (Antiparallel)Define One Ampere CurrentWe, force between two parallel current carrying conductor is given byF=𝜇0

2𝜋r I1I2${\displaystyle F=\frac{{𝜇}_0}{2𝜋r}{I}_1{I}_2}$If, I1=I2=1 A, and r =1m${\displaystyle I_1=I_2=1A,andr=1m}$then F= 𝜇0

2𝜋${\displaystyle F=\frac{{𝜇}_0}{2𝜋}}$where, 𝜇0${\displaystyle {𝜇}_0}$ is the permeability of the medium, whose value is 4𝜋⨯10-7${\displaystyle 4𝜋⨯{10}_{}^{-7}}$so, F= 4𝜋⨯10-7

2𝜋= 2⨯10-7${\displaystyle F=\frac{4𝜋⨯{10}^{-7}}{2𝜋}=2⨯{10}^{-7}}$NThus, One ampere current is that much current which when passed throught two parallel conductors seperated by distance of one metre produces force of 2 ⨯10-7${\displaystyle 2⨯{10}^{-7}}$N between them. >Divergence and Curl of B we know the vector operator (∇)${\displaystyle (\nabla )}$is defines as𝛻=𝚤𝜕

𝜕x+𝚥𝜕

𝜕y+k𝜕

𝜕z. $$𝛻=\widehat{\mathbf{𝚤}}\frac{𝜕}{𝜕x}+\widehat{\mathbf{𝚥}}\frac{𝜕}{𝜕y}+\widehat{\mathbf{k}}\frac{𝜕}{𝜕z}\text{. }$$The divergence of a vector fieldIf magnetic field is considered in cartesian coordinat as B=Bx 𝚤+By𝚥+Bzk$\overrightarrow{B}=B_x\widehat{\mathbf{𝚤}}+B_y\widehat{\mathbf{𝚥}}+B_z\widehat{\mathbf{k}}$, then its divergence at any point is defined bydivB=∇.B=(i𝜕

𝜕x+𝚥 𝜕

𝜕y+k𝜕

𝜕z)⋅(Bx𝚤+By𝚥+Bzk)=𝜕Bx

𝜕x+𝜕By

𝜕y+𝜕Bz

𝜕z$$\begin{array}{c}\mathrm{d}\mathrm{i}\mathrm{v}B=\nabla .\overrightarrow{B}=(\widehat{\mathbf{i}}\frac{𝜕}{𝜕x}+\widehat{\mathbf{𝚥}}\frac{𝜕}{𝜕y}+\widehat{\mathbf{k}}\frac{𝜕}{𝜕z})\cdot (B_x\widehat{\mathbf{𝚤}}+B_y\widehat{\mathbf{𝚥}}+B_z\widehat{\mathbf{k}})\\ =\frac{𝜕B_x}{𝜕x}+\frac{𝜕B_y}{𝜕y}+\frac{𝜕B_z}{𝜕z}\end{array}$$The divergence of a vector field is a scalar field. CurlCurl of magnetic field is defined as curl(B)=𝛻×B$$\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{l}(\overrightarrow{B})=𝛻\times \overrightarrow{B}$$ a

𝛻×B	=|a i 𝚥 k 𝜕 𝜕x 𝜕 𝜕y 𝜕 𝜕z Bx B y Bz |
	=(𝜕Bz 𝜕y-𝜕By 𝜕z)i+(𝜕Bx 𝜕z-𝜕Bz 𝜕x)𝚥+(𝜕B y 𝜕x-𝜕Bx 𝜕y)k

$$\begin{array}{rl}𝛻\times \overrightarrow{B}& =\left|\begin{array}{ccc}\widehat{\mathbf{i}}& \widehat{\mathbf{𝚥}}& \widehat{\mathbf{k}}\\ \frac{𝜕}{𝜕x}& \frac{𝜕}{𝜕y}& \frac{𝜕}{𝜕z}\\ B_x& B_y& B_z\end{array}\right|\\ & =(\frac{𝜕B_z}{𝜕y}-\frac{𝜕B_y}{𝜕z})\widehat{\mathbf{i}}+(\frac{𝜕B_x}{𝜕z}-\frac{𝜕B_z}{𝜕x})\widehat{\mathbf{𝚥}}+(\frac{𝜕B_y}{𝜕x}-\frac{𝜕B_x}{𝜕y})\widehat{\mathbf{k}}\end{array}$$Lorentz ForceWhen a charged particle moves in a magnetic field then it experiences a force which is called Lorentz force. It is found experimentally that this force depends on magnetic field intensity (B)$(\overrightarrow{B})$, amount charge of charged particle (q)$(q)$, velocity of charged particle (v) and angle between the magnetic field and velocity of charged particle (𝜃)$(𝜃)$.Mathematically, a

Lorentz force (F)	=q(v×B)
F	=|q|vBsin𝜃

$\begin{array}{rl}\text{ Lorentz force }(\overrightarrow{F})& =q(\overrightarrow{v}\times \overrightarrow{B})\\ F& =|q|vB\sin 𝜃\end{array}$ Magnetic Scalar Potential: In a region like inside the current carrying conductor curl of B$\overrightarrow{\mathrm{B}}$ is not equal to zero. Hence in that case we cannot introduce scalar potential function as we did in electrostatics. However if we have a current carrying conductor surrounded by empty space, then outside the conductor curl of B=-𝜇0𝛻𝜙m$\overrightarrow{\mathrm{B}}=-{𝜇}_0𝛻{𝜙}_{\mathrm{m}}$.where 𝜙m ${𝜙}_m$ is a magnetic scalar potential. It is used to derive magnetic field in the absence of continuous current distributions. Mathematically,𝜙m=-IΩ

4𝜋[${𝜙}_m=\frac{-I\Omega }{4𝜋}[$ Where Ω$\Omega$ is the solid angle subtended by conductor ]$]$ Vector PotentialFrom Ampere's Circuital law it is obvious that the line integral of magnetic induction around a closed path does not vanish unless it enclose zero current. On the other hand the line integral of electrical field arising from stationary charges always vanishes. Therefore, if we were to define a magnetic scalar potential in a region analogous to electric potential 𝜙$𝜙$ from whichB$\overrightarrow{\mathrm{B}}$ could be derived this magnetic potential would not be single valued function of position unless the region is current free. Because of this short coming it is not generally possible of derive B$\overrightarrow{B}$ from a scalar potential, however a vector potential exists which can be derived. This vector potential is called magnetic vector potential. According to the Biot-Savart law, the divergence of B$\overrightarrow{B}$ is zero i.e.,𝛻⋅B=0 ..................(i)$$𝛻\cdot \overrightarrow{\mathrm{B}}=0..................(i)$$We also know that, 𝛻⋅(𝛻×A)=0$𝛻\cdot (𝛻\times \overrightarrow{\mathrm{A}})=0$ …$\dots$ (ii) From equations (i) and (ii), we getB=𝛻×A ............... (iii)$$\overrightarrow{B}=𝛻\times \overrightarrow{A}...............(iii)$$where A$\overrightarrow{A}$ is the magnetic vector potential and if we know the value of magnetic vector potential, then its curl gives the magnetic field intensity. Here, we have to calculate the value of magnetic vector potential. For this consider a current element Id${\displaystyle Id}$l$\overrightarrow{l}$, the magnetic field at distance r$\mathrm{r}$ from the current element is a

dB=𝜇0 4𝜋Idl×r r3

=-𝜇0 4𝜋Idl×𝛻(1 r)[∵𝛻(1 r)=-r r3]

=𝜇0 4𝜋𝛻(1 r)×Idl

or, dB=𝜇0I 4𝜋(𝛻( 1 r)×dl)..............(iv)

$$\begin{array}{l}\mathrm{d}\overrightarrow{\mathrm{B}}=\frac{{𝜇}_0}{4𝜋}\mathrm{I}\mathrm{d}\overrightarrow{l}\times \frac{\overrightarrow{\mathrm{r}}}{{\mathrm{r}}^3}\\ =\frac{-{𝜇}_0}{4𝜋}\mathrm{I}\mathrm{d}\overrightarrow{l}\times 𝛻\left(\frac{1}{\mathrm{r}}\right)[\because 𝛻(\frac{1}{\mathrm{r}})=\frac{-\overrightarrow{\mathrm{r}}}{{\mathrm{r}}^3}]\\ =\frac{{𝜇}_0}{4𝜋}𝛻\left(\frac{1}{\mathrm{r}}\right)\times \mathrm{I}\mathrm{d}\overrightarrow{l}\\ \text{ or, }\mathrm{d}\overrightarrow{\mathrm{B}}=\frac{{𝜇}_0\mathrm{I}}{4𝜋}\left(𝛻\right(\frac{1}{\mathrm{r}})\times \mathrm{d}\overrightarrow{l})..............(iv)\end{array}$$From vector algebra, we knowa

𝛻×(𝜙A)=(𝛻𝜙)×A +𝜙(𝛻×A)

or, (𝛻𝜙)×A=𝛻×(𝜙A)-𝜙(𝛻×A)

$$\begin{array}{r}𝛻\times (𝜙\overrightarrow{A})=(𝛻𝜙)\times \overrightarrow{A}+𝜙(𝛻\times \overrightarrow{A})\\ \text{ or, }(𝛻𝜙)\times \overrightarrow{A}=𝛻\times (𝜙\overrightarrow{A})-𝜙(𝛻\times \overrightarrow{A})\end{array}$$Applying this in equation (iv), we getor, dB=𝜇0I

4𝜋(𝛻×(dl

r)-1

r(𝛻×dl))$d\overrightarrow{B}=\frac{{𝜇}_{0}I}{4𝜋}(𝛻\times (\frac{d\overrightarrow{l}}{r})-\frac{1}{r}(𝛻\times d\overrightarrow{l}))$As dI$d\overrightarrow{I}$ is not a function of co-ordinates (x,y,z)$(x,y,z)$ at which the magnetic induction is required and the operation 𝛻$𝛻$ represents the differentiation with respect to these co-ordinates, we must have𝛻×dl=0$$𝛻\times \mathrm{d}\overrightarrow{l}=0$$So the above relation becomes,
dB=𝜇0I

4𝜋(𝛻×(dI

r))$$\mathrm{d}\overrightarrow{B}=\frac{{𝜇}_{0}I}{4𝜋}(𝛻\times (\frac{d\overrightarrow{I}}{r}\left)\right)$$The total magnetic field is a

B	=∮dB=𝜇0I 4𝜋∮𝛻×dl r
or, B	=𝛻×∮0𝜇0I 4𝜋dl r ..............(iv)

$$\begin{array}{rl}\overrightarrow{\mathrm{B}}& =\oint \mathrm{d}\mathrm{B}=\frac{{𝜇}_0\mathrm{I}}{4𝜋}\oint 𝛻\times \frac{\mathrm{d}\overrightarrow{l}}{\mathrm{r}}\\ \text{ or, }\overrightarrow{\mathrm{B}}& =𝛻\times \underset{0}{\overset{}{\oint }}\frac{{𝜇}_0\mathrm{I}}{4𝜋}\frac{\mathrm{d}\overrightarrow{l}}{\mathrm{r}}..............(iv)\end{array}$$Comparing equation (iii) and (iv) we getA=∮c𝜇0I

4𝜋dl

r ................. (v)$$\overrightarrow{A}=\underset{c}{\overset{}{\oint }}\frac{{𝜇}_{0}I}{4𝜋}\frac{d\overrightarrow{l}}{r}.................(v)$$which is the required expression of magnetic vector potential. In terms of current density, ∮cIdl=∫VJdV$$\underset{c}{\overset{}{\oint }}\mathrm{I}\mathrm{d}\overrightarrow{l}=\underset{\mathrm{V}}{\overset{}{\int }}\overrightarrow{\mathrm{J}}\mathrm{d}\mathrm{V}$$So, A=𝜇0

4𝜋∫VJdV

r$\overrightarrow{A}=\frac{{𝜇}_0}{4𝜋}\underset{V}{\overset{}{\int }}\frac{\overrightarrow{J}dV}{r}$ ∴A=𝜇0

4𝜋∫vJdV

r ............(v)$$\therefore \overrightarrow{\mathrm{A}}=\frac{{𝜇}_0}{4𝜋}\underset{\mathrm{v}}{\overset{}{\int }}\frac{\overrightarrow{\mathrm{J}}\mathrm{d}\mathrm{V}}{\mathrm{r}}............(v)$$Equations (v) and (vi) are used to derive magnetic induction B$\overrightarrow{B}$ at any point from the magnetic potential A$\overrightarrow{A}$ at that point.